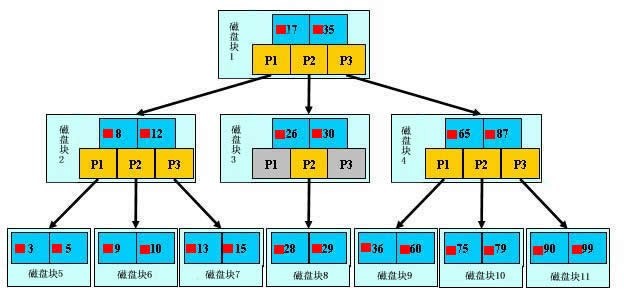
B-Tree也叫B树,这是一种专门为磁盘或者其他直接存储设备而设计的多叉平衡树,他的每个节点是由关键字和指向子节点的指针构成的。
树的阶和度
树的阶:指的是一颗树中节点含有子节点的最大数量,这里我们用m来表示树的阶。
树的度:指的是一颗树中节点含有子节点的最小数量,这两我们用t来表示树的度
B树中内节点(非根节点和非叶子节点)的t >= 2。
以树的阶m为维度的B-Tree有以下特性
- 每个节点最多含有m个孩子。
- 除根节点和叶子节点每个节点含有[m/2]个孩子。
- 如果根节点不是叶子节点,那B树的根节点至少要有两个孩子,B树只有一个根节点的情况除外。
- 所有的叶子都在同一层,如果把叶子节点理解为空指针NULL,那么叶子节点不包含任何关键字信息和指针,如果把叶子节点理解为最后一层有数据的节点,那么叶子节点肯定含有关键字和指向NULL的指针。
- 每个节点含有n个关键字,那么将有以下几条子特性。
(a). B树中的每个节点中的关键字是有顺序的,如果Ki(i = 1…n)为关键字,那么将有 Ki-1 < Ki。
(b). 假设B树中的每个节点中的指针为Pi(i = 0…n),那么Pi指向的孩子中所有接的关键字K将满足 Ki-1 < K < Ki。
(c). 由(a)(b)两条特性可知一个节点中关键字个数和指针个数的关系(有多少指针就有多少的孩子),即如果一个节点有n个关键字,那么这个节点将有n+1个(看i的起始值)指针或者是n+1个孩子。再由特性2可知[m/2]其实就是树的度。所以一个节点的关键字n必须满足: t-1 <= n <= m-1 或者是 [m/2]-1 <= n <= m-1。
以树的度t为维度的B-Tree有以下特性
由m定义的特性中不难看出,B树的度和阶是有对应关系的,即 t=[m/2], m=2t。所以通过t来介绍的B树的特性是与m介绍B树的特性是一一对应的。
- 非叶子节点至少还有t个孩子。至少有t-1个关键字。
- 非叶子节点至多还有2t个孩子,至多有2t-1个关键字。
- 同m特性中的3。
- 同m特性中的4。
- 每个节点关键字的个数满足 t-1 <= n <= 2t-1
B-Tree的高度
树的高度会影响磁盘定位寻址的效率,如果一个树的高度很大,势必会增加磁盘IO次数,将会影响查找性能。那么B树的查找性能的瓶颈在哪里呢?或者说B树的最大高度是多少?下面是B树的高度公式。
公式:一颗含有n个关键字、度是t、高度h的B树满足公式:h <= logt((n+1)/2) 或者 h <= logt((n+1)/2) + 1, 加不加1要看如何定义层数的起始点,从0开始不加1,从1开始就加1
推倒过程:
基本思想是用所有节点个数 * 每个节点关键字个数 <= n,而每个节点至少有t-1个关键字。
- 第1层根节点最少有1个关键字,因为根至少有两个孩子。 关键字个数 1
- 第2层最少有 2 个节点,每个节点至少有t-1个关键字。 关键字个数 2 *(t-1)
- 第3层最少有 2t 个节点,每个节点至少有t-1个关键字。 关键字个数 2t * (t-1)
- 第4层最少有 2t^2,每个节点至少有t-1个关键字。 关键字个数 2t^2 * (t-1)
- 第h层最少有 2t^(h-2),每个节点至少有t-1个关键字。 关键字个数 2t^(h-2) * (t-1)
所以有 1 + 2(t-1)+ 2t (t-1) + 2t^2 (t-1) + … + 2t^(h-2) (t-1) <= n
得 1 + (t-1)∑2t^(i-2) = 1 + 2(t-1)(t^(h-1) - 1 / t - 1) = 1 + 2t^(h-1) <= n, 注意求和公式i从1开始到h。
最后得出 h <= logt((n-1)/2) + 1
B-Tree的插入操作
一颗m阶的B树插入操作的思想:
做插入操作的时候要考虑插入空间的上限,所以通过m阶来理解B-Tree树的插入操作比较容易。m阶的B树的节点最多有m-1个关键字。当执行插入操作操作的时候,是自底向上进行分裂操作,每次找到对应的叶子节点进行插入时,判断当前空间是否已满。
- 如果过空间足够,直接插入,但是要保证关键字K的顺序。
- 如果空间已满,需要进行分裂操作,将中间关键字上移,成为父亲节点,比中间关键字小的成为新的左孩子,比中间关键字大的成为新的右孩子。
- 如果在执行分裂上移操作时,要上移到的空间已经满了,同样执行分裂操作。
插入操作比较简单,不进行图解展示,以后附上B树的插入操作实现的代码。
B-Tree的删除操作
B-Tree删除操作的基本思想:
做删除操作的时候要考虑删除空间的下限,因为B-tree每个内节点至少要有t-1或者是[m/2]-1个关键字,根节点至少要有1个关键字,如果删除时关键字的个数不满足B树特性时,左右节点要进行合并等操作。具体操作如下。
- 删除叶子节点中的关键字Ki:
(a) 如果删除Ki所在的节点的关键字个数大于[m/2],则直接删除Ki和对应的指针。
(b) 如果删除Ki所在的节点的关键字个数等于[m/2],要看左右兄弟节点关键字个数是否足够(>[m/2])
(b.1) 如果足够,向父亲接一个关键字,即空间足够兄弟节点和本节点的分隔关键字,兄弟节点中最大的关键字(左兄弟)或者最小的关键字(有兄弟)上移至父亲节点中。
(b.2) 如果左右兄弟节点的关键字个数都刚刚足够,则不能向父亲节点借用关键字,需要进行合并操作,此时下移父节点中。 要合并的两个节点的分隔关键字,生成一个新的节点,此时如果合并下移父节点关键字之后造成父节点不满足最小关键字个数,则将该父亲节点当成叶子节点进行相同操作。同b.1和b.2步骤。 - 删除非叶子节点中的关键字Ki。需要看Pi-1所指向的左孩子或者是Pi所指向的右孩子,将左孩子中最大的关键字或者右孩子中最小的关键字上移至删除Ki的地方。那就相当于删除了Pi-1或者Pi指向节点中的关键字,然后再看这个节点是否为叶子节点在重复1,2步骤。
暂不进行删除操作图解。
